 DIY Builds
DIY Builds
 DIY Builds
DIY Builds

 Photo: David Iglesias
Photo: David Iglesias
Euclid was famous as the author of the Elements, a treatise that taught geometry through rigorous proofs of theorems.

Birch plywood Birch plywood is one of the most widely used skate ramp surfacing materials. Birch is very tense yet flexible and also highly...
Read More »
Building a garage by yourself is a serious project but can be done with enough motivation, planning, and knowledge. By taking on the project...
Read More »

Top 5 Tips to Prevent Mould in your Shed Ventilate your shed. Make sure everything is dry. Add moisture absorbers or a dehumidifier. Keep...
Read More »
So, what is ACX plywood? ACX plywood is a version of a plywood panel that has a very specific makeup, with one rough face and one sanded face on...
Read More »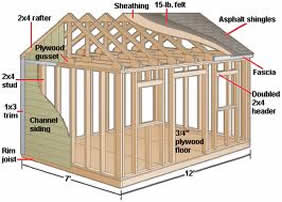
Euclid's axioms 1 Given two points there is one straight line that joins them. 2 A straight line segment can be prolonged indefinitely. 3 A circle can be constructed when a point for its centre and a distance for its radius are given. 4 All right angles are equal. 5 If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which the angles are less than the two right angles. Euclid's common notions 6 Things equal to the same thing are equal. 7 If equals are added to equals, the wholes are equal. 8 If equals are subtracted from equals, the remainders are equal. 9 Things that coincide with one another are equal. 10 The whole is greater than a part. The subject of Book II has been called geometric algebra because it states algebraic identities as theorems about equivalent geometric figures. Book II contains a construction of “the section,” the division of a line into two parts such that the ratio of the larger to the smaller segment is equal to the ratio of the original line to the larger segment. (This division was renamed the golden section in the Renaissance after artists and architects rediscovered its pleasing proportions.) Book II also generalizes the Pythagorean theorem to arbitrary triangles, a result that is equivalent to the law of cosines (see plane trigonometry). Book III deals with properties of circles and Book IV with the construction of regular polygons, in particular the pentagon. Book V shifts from plane geometry to expound a general theory of ratios and proportions that is attributed by Proclus (along with Book XII) to Eudoxus of Cnidus (c. 395/390–342/337 bce). While Book V can be read independently of the rest of the Elements, its solution to the problem of incommensurables (irrational numbers) is essential to later books. In addition, it formed the foundation for a geometric theory of numbers until an analytic theory developed in the late 19th century. Book VI applies this theory of ratios to plane geometry, mainly triangles and parallelograms, culminating in the “application of areas,” a procedure for solving quadratic problems by geometric means. Get a Britannica Premium subscription and gain access to exclusive content. Subscribe Now

A beam is the main load-bearing structural element of a roof. It supports the weight of joists and other building elements. A joist is a horizontal...
Read More »
Made from either steel or galvanized aluminum, metal outdoor sheds provide durability at a very cost-effective price; although, metal is...
Read More »
Books VII–IX contain elements of number theory, where number (arithmos) means positive integers greater than 1. Beginning with 22 new definitions—such as unity, even, odd, and prime—these books develop various properties of the positive integers. For instance, Book VII describes a method, antanaresis (now known as the Euclidean algorithm), for finding the greatest common divisor of two or more numbers; Book VIII examines numbers in continued proportions, now known as geometric sequences (such as ax, ax2, ax3, ax4…); and Book IX proves that there are an infinite number of primes. According to Proclus, Books X and XIII incorporate the work of the Pythagorean Theaetetus (c. 417–369 bce). Book X, which comprises roughly one-fourth of the Elements, seems disproportionate to the importance of its classification of incommensurable lines and areas (although study of this book would inspire Johannes Kepler [1571–1630] in his search for a cosmological model). Books XI–XIII examine three-dimensional figures, in Greek stereometria. Book XI concerns the intersections of planes, lines, and parallelepipeds (solids with parallel parallelograms as opposite faces). Book XII applies Eudoxus’s method of exhaustion to prove that the areas of circles are to one another as the squares of their diameters and that the volumes of spheres are to one another as the cubes of their diameters. Book XIII culminates with the construction of the five regular Platonic solids (pyramid, cube, octahedron, dodecahedron, icosahedron) in a given sphere, as displayed in the animation. The unevenness of the several books and the varied mathematical levels may give the impression that Euclid was but an editor of treatises written by other mathematicians. To some extent this is certainly true, although it is probably impossible to figure out which parts are his own and which were adaptations from his predecessors. Euclid’s contemporaries considered his work final and authoritative; if more was to be said, it had to be as commentaries to the Elements.

Table Salt - Using salt to kill weeds is a common do-it-yourself solution. When salt is absorbed by plant root systems, it disrupts the water...
Read More »
EPDM membranes are fast-becoming the roofing industry's go-to alternative to felt and other outdated roofing materials. The composition of EPDM as...
Read More »

Where can you get paid to be an online friend? Rent a Friend. Rent a Friend is a legit site that does exactly what it says in its name, in that it...
Read More »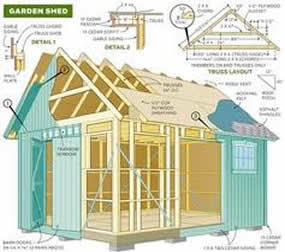
These are! They guide you every step of the way to complete your dream shed.
Learn More »
A quality-built portable shed starts at the size of 8' x 12' and can be made to the largest size of 16' x 48 '.
Read More »